Stochastic in nature, heard of it. Let us see in this article how pytorch can help us in probability distribution. A statistical function that gives the probability or chances of occurrence of different possible outcomes for an experiment. Going through a event or a series of events, what are the chances of a particular value to be taken by a variable is given through this distribution.
Let us move into concepts of training neural network models. We all know a neural network model is just of combination of different weights at different steps. These are weights and biases that perform the magic. We know the neural network itself modifies the weights and at the end come up with such a combination that can give us the nearest possible perfect solution to the problem. But the interesting part is at the beginning which is the initial weights provided at different layers. Weight initialization can be performed using random weight initialization based on a distribution using Bernoulli, Multinomial and normal distribution.
To execute a neural network, a set of initial weights needs to passed to backpropagation layer to compute loss function. Let us have a look at all types of approaches to initialize weights. If the use case requires reproducing the same set of results to maintain consistency, then a manual seed needs to be set.
Uniform Distribution
As we have seen in the article of tensors, the randn() function is used to form a tensor having normal distribution. But random numbers can also be generated following uniform distribution. The probability density function of continuous uniform distribution is defined by

import torch
torch.manual_seed(1234)
torch.randn(4, 4)
'''
tensor([[-0.1117, -0.4966, 0.1631, -0.8817],
[ 0.0539, 0.6684, -0.0597, -0.4675],
[-0.2153, 0.8840, -0.7584, -0.3689],
[-0.3424, -1.4020, 0.3206, -1.0219]])
'''
torch.Tensor(4, 4).uniform_(0, 1)
'''
tensor([[0.2837, 0.6567, 0.2388, 0.7313],
[0.6012, 0.3043, 0.2548, 0.6294],
[0.9665, 0.7399, 0.4517, 0.4757],
[0.7842, 0.1525, 0.6662, 0.3343]])
'''
Binomial Distribution
Binomial distribution is one, in which number of trials can be more than one. The binomial distribution is applicable when the outcome is twofold and the experiment is repetitive. It belongs to the family of discrete probability distribution, where the probability of success is defined as 1 and the probability of failure is 0. The binomial distribution is used to model the number of successful events over many trials
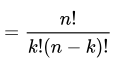
Here n is number of trials and k is the number of successes.
from torch.distributions.binomial import Binomial
dist = Binomial(100, torch.tensor([0.2, 0.8, 1]))
dist.sample()
# tensor([ 16., 76., 100.])
Bernoulli Distribution
In statistics, Bernoulli distribution is considered as discrete probability distribution. For discrete probability distribution, we calculate probability mass function instead of probability density function.
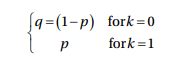
import torch
from torch.distributions.bernoulli import Bernoulli
dist = Bernoulli(torch.tensor([0.3, 0.6, 0.9]))
dist.sample()
# tensor([0., 1., 1.])
torch.bernoulli(torch.Tensor(4, 4).uniform_(0, 1))
'''
tensor([[0., 1., 1., 1.],
[1., 0., 0., 0.],
[0., 0., 1., 1.],
[0., 0., 0., 0.]])
'''
p = torch.tensor(0.6)
dist = Bernoulli(p)
coin_tosses = dist.sample((10,))
print(coin_tosses)
num_heads = torch.sum(coin_tosses==1)
num_tails = torch.sum(coin_tosses==0)
prob_heads = num_heads/10
prob_tails = num_tails/10
print(prob_heads, prob_tails)
'''
tensor([1., 0., 0., 1., 1., 0., 1., 1., 1., 1.])
tensor(0.7000) tensor(0.3000)
'''
Multinomial Distribution
Multinomial distribution gives the probability of any particular number of successes for the various categories. It generalizes the binomial distribution. It models the probability of counts for each side of a k sided die rolled n times.

In multinomial distribution, we can opt with a replacement or without a replacement. By default, multinomial distribution is performed without replacement. To perform replacement, an extra argument needs to be specified. It outputs the result as index position for the tensors.
torch.multinomial(torch.Tensor([10, 10, 13, 10, 34, 45, 65, 67, 87, 89, 87, 34]), 3)
# tensor([11, 10, 8])
torch.multinomial(torch.Tensor([10, 10, 13, 10, 34, 45, 65, 67, 87, 89, 87, 34]), 5, replacement=True)
# tensor([8, 7, 7, 8, 0])
Normal Distribution
Weight initialization from normal distribution is a way used in fitting a neural network, fitting a deep neural network, CNN and RNN. The normal distribution is bell shaped. The bell-curve values near to the mean have higher probabilities.
The general form of probability density function is

from torch.distributions.normal import Normal
dist = Normal(torch.tensor([100.0]), torch.tensor([10.0]))
dist.sample()
# tensor([114.7997])
torch.normal(mean=torch.arange(1., 11.), std=torch.arange(1, 0, -0.1))
''' tensor([1.9723, 2.9941, 2.1138, 3.8819, 5.1138, 6.2424, 7.0356, 8.0728,
8.8455, 9.9692])
'''
torch.normal(mean=0.5, std=torch.arange(1., 6.))
# tensor([ 0.8364, 0.6838, -2.1869, -0.6363, 6.9129])
This article includes the sampling distribution and methods of generating random numbers from distributions. The description of statistical distributions supported by pytorch and the places where they are applicable are given here.
That’s it!
Thank you!
— Akhil Soni
